CONCEPTO:
Es una rama de las matemáticas que se ocupan de figuras, líneas y formas, tiene muchas aplicaciones prácticas en el campo de la arquitectura. Una comprensión de la geometría es completamente esencial para el diseño arquitectónico, tanto en un sentido práctico (tales como el cálculo de carga segmentos de una estructura) y en consideraciones estéticas (tales como simetría de un edificio o escala con su entorno). La necesidad de la enseñanza de la geometría en el ámbito escolar responde, en primer lugar, al papel que la geometría desempeña en la vida cotidiana.
Un conocimiento geométrico básico es indispensable para desenvolverse en la vida Cotidiana: para orientarse reflexivamente en el espacio; para hacer estimaciones sobre formas y distancias; para hacer apreciaciones y cálculos relativos a la distribución de los objetos en el espacio.
La enseñanza de la Geometría ha tenido tradicionalmente un fuerte carácter deductivo. En educación secundaria, la Geometría se ha venido apoyando en el lenguaje del álgebra, en el álgebra vectorial. En primaria, aún sin ese carácter algebraico, formal, se ha fomentado excesivamente el aprendizaje memorístico de conceptos, teoremas y fórmulas; la simple apoyatura de unos conceptos en otros previos; y la temprana eliminación de la intuición como instrumento de acceso al conocimiento geométrico, tratando de acelerar la adquisición de tales conceptos, teoremas y fórmulas, como si en ellas estuviera condensado el verdadero saber geométrico.
Las investigaciones sobre el proceso de construcción del pensamiento geométrico parecen indicar, no obstante, que éste sigue una evolución muy lenta desde unas formas intuitivas iniciales de pensamiento, hasta las formas deductivas finales, y que éstas corresponden a niveles escolares bastante más avanzados que los que estamos considerando aquí. De manera que nosotros entendemos que en Educación Primaria hay que escapar de las interpretaciones deductivistas e ir a una Geometría de carácter experimental intuitiva.
DISTANCIA ENTRE DOS PUNTOS EN EL ESPACIO
Los razonamientos sobre la construcción de los ejes coordenados son igualmente válidos para un punto en el espacio y un grupo de ordenadas de números, sin más que introducir una tercera recta perpendicular a los ejes x e y: el eje z. Resultando una única ecuación lineal del tipo:
ax + by + cz = 0
Representa en el espacio un plano. Si se pretende representar mediante ecuaciones una recta en el espacio tridimensional necesitaremos especificar, no una, sino dos ecuaciones lineales como las anteriores. De hecho toda recta se puede escribir como intersección de dos planos. Así una recta en el espacio podría quedar representada como:
Si bien, por el momento se ha trabajado únicamente con dos variables, el incluir una variable más (z), implica la ampliación del sistema de coordenadas y el establecimiento de ciertas reglas para la graficación tridimensional.
El sistema tridimensional de coordenadas rectangulares se forma a partir de tres ejes perpendiculares entre sí, de manera que existe un eje que se proyecta hacia delante, es decir, que se "sale" del papel. Al igual que en el dibujo tridimensional, los ejes se pueden trazar como una vista en isométrico o axonométrico.
ECUACIÓN
La distancia entre dos puntos es igual al módulo del vector que tiene de extremos dichos puntos.
1).Hallar la distancia entre los puntos A(1, 2, 3) y B(−1, 2, 0).
PUNTO MEDIO EN EL ESPACIO
Coordenadas del punto medio de un segmento
Sean A (x1, y1, z1) y B (x2, y2, z2) los extremos de un segmento, el punto medio del segmento viene dado por:
Ejemplo
Dados los puntos A (3, −2, 5) y B (3, 1, 7), hallar las coordenadas del punto medio del segmento que determinan.
ECUACION DE UNA RECTA EN EL ESPACIO
Ecuación de la recta
Sea P(x1, y1) es un punto de la recta r y vector u su vector director, el vector vector director tiene igual dirección que vector u, luego es igual a vector u multiplicado por un escalar:
Ecuaciones paramétricas de la recta
Operando en la ecuación vectorial de la recta llegamos a la igualdad:
Esta igualdad se verifica si:
Ecuaciones continuas de la recta
Despejando e igualando λ en las ecuaciones paramétricas se tiene:
Ecuaciones implícitas de la recta
Una recta puede venir determinada por la intersección de los planos.
Si en las ecuaciones continuas de la recta quitamos denominadores y pasamos todo al primer miembro, obtenemos también las ecuaciones implícitas.
EJEMPLOS
1.- Hallar las ecuaciones paramétricas, en forma continua e implícitas de la recta que pasa por el punto A = (1, 2, 1) y cuyo vector director es
2.- Hallar las ecuaciones paramétricas, en forma continua e implícita de la recta que pasa por los puntos A (1, 0, 1) y B (0, 1, 1).
Sea r la recta de ecuación:
¿Pertenecen a r los puntos A (0, −2, −2) y B (3, 2, 6)?







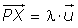





















No hay comentarios:
Publicar un comentario